http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t1-conicas/2-Parabola/index.html
http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t1-conicas/4-Hiperbola/index.html
ELIPSE:Una elipse es el conjunto de puntos(x,y) cuya suma de distancias a dos puntos distintos prefijados (llamados focos) es constante.
La recta que pasa por los focos corta a la elipse en dos puntos llamados vértices. La cuerda que une los vértices es el eje mayor de la elipse y su punto medio el centro de la elipse. La cuerda perpendicular al eje mayor y que pasa por el centro se llama eje menor de la elipse.
Para visualizar la definición de la elipse, basta imaginar dos chinches clavados en los focos y un trozo de cuerda atada a ellos. Al ir moviendo un lápiz que tensa esa cuerda, su trazo irá dibujando una elipse, como se muestra en la figura 1.
figura 1
La forma canónica de la ecuación de una elipse de centro (h,k) y ejes mayor y menor de longitudes 2a y 2b respectivamente, con a>b , es
Observación : de la figura 2, podemos deducir que d(V1,F1) + d(V1,F2)= 2a, (tomando P=V1)es decir, 2a es la constante a la que se refiere la definición.
Los focos están en el eje mayor a c unidades del centro con 
,y el eje mayor es horizontal.En el caso de que el eje mayor sea vertical la ecuación toma la forma:
,y el eje mayor es horizontal.En el caso de que el eje mayor sea vertical la ecuación toma la forma: 
Observación : la demostración de este teorema no es complicada, basta aplicar la definición y la fórmula de distancia (figura 2
Simplificando
Pero,y así obtenemos la ecuación canónica de la elipse
y así obtenemos la ecuación canónica de la elipse Teorema (propiedad de reflexión)
La recta tangente a una elipse en un punto P forma ángulos iguales con las rectas que pasan por P y por alguno de los focos.
figura 3
Ejemplo 1 Hallar la ecuación canónica de la elipse
Trazar su gráfica identificando los vértices, los focos, el centro y la excentricidad.
Solución
Para hallar la ecuación canónica debemos completar el cuadrado de la expresión en ambas variables x e y .
De donde obtenemos que el centro es (1,-2), el valor de a=4 ( es la longitud mayor, esto nos dice que la elipse es vertical), el valor de b=2 y el valor de está dado por :
Y así, los focos están dados por 
y los vértices por 
Por último, la excentricidad es
y los vértices por 
Por último, la excentricidad es 
La gráfica se muestra en la figura 4.
Definición (excentricidad)
La excentricidad e de una elipse está dada por el cociente
Parábola
Ahora, vamos a deducir las ecuaciones de las secciones cónicas a partir de su definición como lugares geométricos y no como la intersección de un cono con un plano, como se hizo en la antigüedad. Ya conocemos que la gráfica de una función cuadrática
con
, es una parábola. Sin embargo, no toda parábola es la gráfica de una función, como podemos concluir de la siguiente definición. Definición
El punto medio entre el foco y la directriz se llama vértice, la recta que pasa por el foco y por el vértice se llama eje de la parábola.Se puede observar en la figura 1 que una parábola es simétrica respecto a su eje.
Teorema (ecuación canónica de la parábola)
La forma canónica de la ecuación de una parábola con vértice 
y directriz es:
El eje de la parábola es vertical y el foco F está a 
unidades (orientadas) del vértice. Si p>0 , la parábola abre hacia arriba y el foco está en 
; si p<0 , la parábola abre hacia abajo y el foco está en 
Si la directriz es 
(eje horizontal), la ecuación es
unidades (orientadas) del vértice. Si p>0 , la parábola abre hacia arriba y el foco está en 
; si p<0 , la parábola abre hacia abajo y el foco está en 
Si la directriz es 
(eje horizontal), la ecuación es 
El eje de la parábola es horizontal y el foco F está a unidades (orientadas) del vértice. Si p>0 , la parábola abre hacia la derecha y el foco está en 
; si p<0 parábola abre hacia la izquierda y el foco está en 
unidades (orientadas) del vértice. Si p>0 , la parábola abre hacia la derecha y el foco está en 
; si p<0 parábola abre hacia la izquierda y el foco está en 
Observación : la demostración de este teorema no es difícil, basta aplicar la definición y la fórmula de distancia (figura 1).Para el caso en el cual el eje de la parábola es vertical, tenemos que
Ejemplo 1.
Trazar la gráfica y hallar la ecuación canónica, el vértice, el foco y la directriz de la parábola cuya ecuación es
Solución
Para hallar la ecuación canónica debemos completar el cuadrado en a. De la ecuación de la parábola tenemos que
De donde obtenemos que p=1 y el vértice v=(2,3) , por lo tanto, la parábola abre hacia la derecha y tiene el foco en F=(3,3) , la recta directriz es x=1 . La gráfica se muestra en la figura 2.
Hipérbola
Las hipérbolas aparecen en muchas situaciones reales, por ejemplo, un avión que vuela a velocidad supersónica paralelamente a la superficie de la tierra, deja una huella acústica hiperbólica sobre la superficie. La intersección de una pared y el cono de luz que emana de una lámpara de mesa con pantalla troncocónica, es una hipérbola.
La definición de la hipérbola como lugar geométrico es similar a la dada para la elipse, como vemos en seguida
Definición
Una hipérbola es el conjunto de puntos P(x,y) para los que la diferencia de sus distancias a dos puntos distintos prefijados (llamados focos) es constante.
La recta que pasa por los focos corta a la hipérbola en dos puntos llamados vértices. El segmento recto que une los vértices se llama eje transversal y su punto medio es el centro de la hipérbola. Un hecho distintivo de la hipérbola es que su gráfica tiene dos partes separadas, llamadas ramas.
Teorema (ecuación canónica de la hipérbola)
La ecuación canónica de la hipérbola con centro en (h,k) es
con eje transversal horizontal. Y
con eje transversal vertical.
Los vértices están a una distancia de a unidades del centro y los focos a una distancia de c unidades del centro. Además
Resumiendo:
Si el eje transversal de la hipérbola es horizontal entonces
El centro está en (h,k)
Si el eje transversal de la hipérbola es vertical entonces
El centro está en (h,k)
Una ayuda importante para trazar la gráfica de una hipérbola son sus asíntotas. Toda hipérbola tiene dos asíntotas que se intersecan en su centro y pasan por los vértices de un rectángulo de dimensiones 2a y 2b y centro en (h,k) .El segmento recto de longitud 2b que une
se llama eje conjugado de la hipérbola. El siguiente teorema identifica la ecuación de las asíntotas. Teorema (Asíntotas de una hipérbola)
Si la hipérbola tiene un eje transversal horizontal, las ecuaciones de las asíntotas son
y si el eje transversal es vertical, las ecuaciones de las asíntotas son
Observación : las asíntotas de la hipérbola coinciden con las diagonales del rectángulo de dimensiones 2a y 2b centro (h,k) Esto sugiere una forma simple de trazar tales asíntotas
Definición (excentricidad de una hipérbola)
Si la excentricidad es grande los focos están cerca del centro y las ramas de la hipérbola son casi rectas verticales. Si la excentricidad es cercana a uno los focos están lejos del centro y la ramas de la hipérbola son más puntiagudas.
La propiedad reflectora de la hipérbola afirma que un rayo de luz dirigido a uno de los focos de una hipérbola se refleja hacia el otro foco (figura 2).
Teorema (propiedad de reflexión)
La tangente en un punto P de una hipérbola es la bisectriz del ángulo formado por lo segmentos que unen este punto con los focos.
Ejemplo 1
Hallar la ecuación canónica, los focos, los vértices, la excentricidad y las asíntotas de la hipérbola cuya ecuación es
Solución
Completando el cuadrado en ambas variables
Por tanto, el centro está en (2,-3) El eje de la hipérbola es horizontal a=1, b=3 y
Los vértices están en (1,-3), (3,-3) los focos en 
y 
y 
la excentricidad es
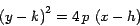
No hay comentarios:
Publicar un comentario